Explanatory Note: The text below contains some recommendations on how to develop a modern motor controller. It contains some recommendations to help the designer to get the job done relatively quickly without an infinite struggle with doubts and discussions at every possible aspect of the project. The text does not pretend to be academically rigorous, rather it is more about practical ways of solving particular problems. Quoting Captain Barbossa: “This is more a set of guidelines than actual rules.”
Many of us come to this idea at one moment of our lives – to the idea of developing a custom brushless motor controller. It may arise for different reasons: you’re building a high-end vehicle with very specific requirements or you just need a decent controller. There is a certain set of steps that are to be taken to achieve this goal, all of which involve knowledge from different fields. It may be difficult for a single person to be competent in all these fields so this text describes an easier way of completing this challenge successfully. It reduces the skills and competencies needed and also drastically reduces the development time.
Let’s list all the stages of custom ESC development (supposing that high-level requirements like power level, input voltage range etc. have already been put in place):
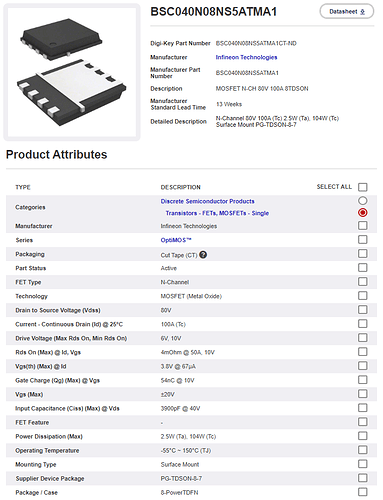
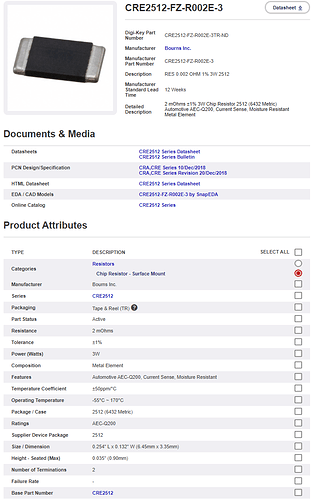
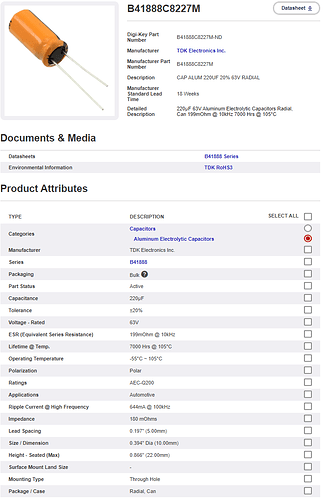
- Pick up the main components: power transistors, transistor driver, MCU, DC-DC converters, communication interface drivers and connectors etc.
- Carefully read all the datasheets to look for possible conflicts. (Just for reference, the datasheet for a modern transistor driver IC like DRV8350 from TI is a 100 pages long complex technical document).
- Create a schematic of the whole controller.
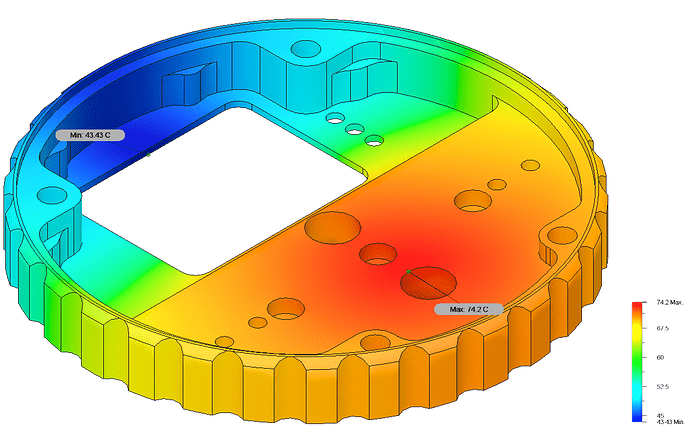
- Carefully think over the component arrangements taking into account things like possible electromagnetic issues, cooling and housing means, the ease of reach of the connectors, etc.
- Route the PCB; possibly, several times due to the errors made in the previous stages.
- Design a housing that is possible to manufacture using a selected technology (be it 3D printing or milling or whatever else).
All these steps, although they may not be that simple, take a finite amount of time. The last ones, however, may take forever and never be completed:
- Software development and debugging.
- A GUI will be most probably needed to configure the controller.
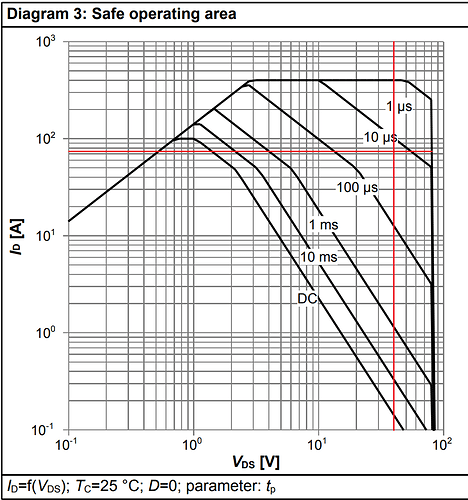
The problem with programming and debugging motor controllers (and power electronics in general) is that they require the developer to be familiar with motor control theory, linear algebra, common electrodynamics and, of course, embedded real-time programming. The means of debugging such systems is very limited too, as the process under control is very fast and involves high-energy transitions. It is impossible to just halt the MCU and inspect its internal state or to use other conventional debugging methods like printing out the variables to the serial output. Besides, if something goes wrong it often causes hardware damage so perfect repair and soldering skills would be helpful.
A few of words about reliability should be made. In many cases, a controller is intended to control a motor mounted on some kind of aerial vehicle. This imposes special reliability requirements because a controller failure may lead to catastrophic consequences, not least the aircraft will be most probably critically damaged. This means that the software must be very reliable which can only be achieved by following standards like MISRA and doing lots of testing.
Conspicuously, the development of a motor controller from scratch is a major effort and one in which results are not guaranteed. But there is a way to avoid most of the challenges involved: use an integrated module for PMSM/BLDC motor control to do all the heavy lifting. This is what Zubax Mitochondrik LV does. Of course, even with this help, the whole development process will be hardly a piece of cake but it does simplify it a lot. The main advantages are:
- The only components that have to be selected are the power stage components, interface ICs and connectors. Generally, the hardest part is selecting the power transistors, proper capacitors and shunt resistors for the current measurements.
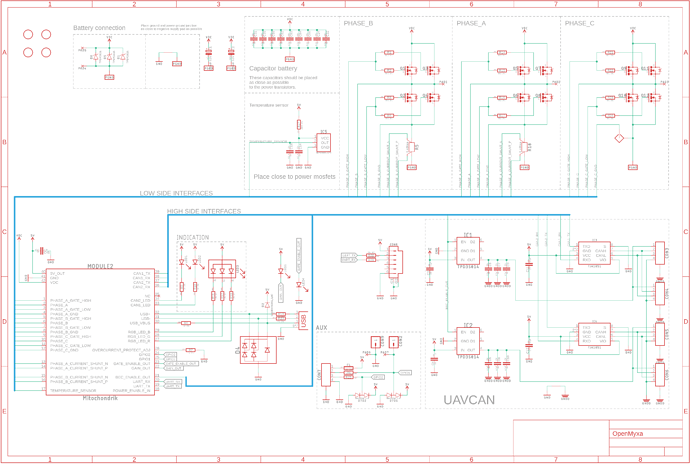
- The schematic and PCB design are greatly simplified as all the complex circuitry is embedded into the module.
- There is no need to mess with the DC-DC converter design as it is embedded into the module.
- And most importantly; no programming needed. Mitochondrik LV runs Télega software which uses advanced and sophisticated algorithms to control the motor. Also, there is a standard GUI tool for Télega-based controllers already so no additional PC-software development is needed either.
Therefore, the application of Mitochondrik LV in motor controller development leaves the designer with many fewer problems to solve.
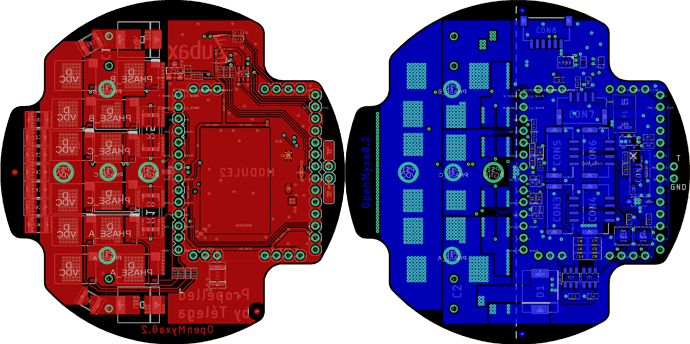
Below is an example of controller development using Mitochondrik LV using a Zubax Komar controller.
The initial requirements of the controller are:
- Input voltage range: 20 – 50.4 V.
- Continuous power output: 2 – 2.8 kW with a 12S battery where the range of possible battery voltages is 40 – 50.2 V.
- Dimensional requirements: Circular and comparable in size to a compact 2 kW-rated motor like the T-motor MN5212.